Find the solutions (roots) of a
quadratic equation using the graphing calculator.
Consider the following examples:
| 1. |
Using the ZERO Command |
| |
Solve: 
Since this equation is set equal to zero, the roots will be the locations
where the graph crosses the x-axis (if the roots
are real numbers).
(Remember that the x-axis is really
just y = 0.)
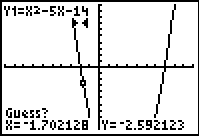
1. Set 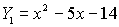
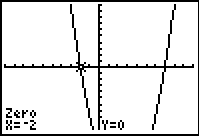
2. Use the ZERO command to find the roots -- 2nd TRACE (CALC), #2 zero
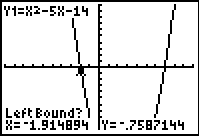
3. Left bound? Move
the spider as close to the root (where the graph crosses
the x-axis) as possible. Hit the left arrow
to move to the "left" of the root. Hit ENTER. A "marker"
► will be set to the
left of the root.
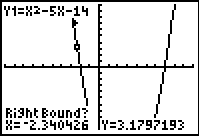
4. Right bound? Move
the spider as close to the root (where the graph crosses
the x-axis) as possible. Hit the right
arrow to move to the "right" of the root. Hit ENTER. A "marker"
◄ will be set to the
right of the root.
5. Guess? Just
hit ENTER.
6. Repeat the entire process to find the second
root (which in this case happens to be x = 7).
Answer:
one of the roots is x = -2
 |
Standard 10 x 10 window

 |
2. |
Using
the INTERSECT Command |
| |
Solve: 
Since this equation is NOT set equal to zero,
the ZERO command cannot be used to look for roots(unless you re-write the
equation so that it IS set equal to zero).
If you do not want to re-write the
equation, solve using the intersect command to find the points where the two
expressions intersect (if the roots are real numbers):
1. Set 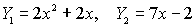
2. Use the intersect command to find the roots, 2nd TRACE (CALC), #5 intersect.
3. First Curve? Move
the spider close the point of intersection that you want
to find. Hit ENTER.
4. Second Curve? Just
hit ENTER.
5. Guess? Just
hit ENTER.
6. Repeat the entire process to find the second
root (which in this case happens to be x = 2).
Answer:
one of the roots is x = 0.5
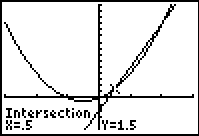 |
Window [-3,3] x [-5,15]

|
3. |
Only One Root? |
| |
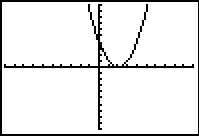
Solve: 
When graphed, this equation only
intersects the x-axis in one location. This tells
you that this root repeats itself.
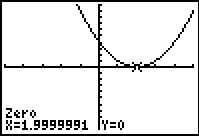 |
If a reading appears such as
1.9999991, the actual answer is most likely the
number 2. Check your assumption that the
answer is 2 by substituting 2 into the original
equation to see if it satisfies the equation. |
|
Standard 10 x 10 window
 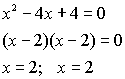
|
4. |
What if
the graph does not intersect the x-axis???
(or the "intersect" option shows no intersections) |
| |
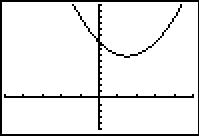
Solve: 
When graphed, this equation does NOT
intersect the x-axis. This tells you that the
roots of this equation are complex
(imaginary) values. Dig out
the quadratic formula to find the roots.
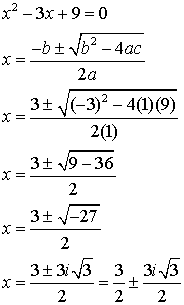
|
Window [-5,5] x [-5,15]
 |
5. |
Need to
WRITE a quadratic equation from a graph? |
| |
If you are given the
visual graph of a quadratic equation and you are given (or can identify) at
least 3 points, you can use the Quadratic Regression
process to create the equation of the graph.
Write the equation of the
parabola shown at the right, given that the points (0,2),
(-1,9) and (3,5) are on the graph.
1. Enter the points into
L1 and
L2 (x-coordinate
in L1 and
matching y-coordinate in L2)
(See Basic Commands for Stats if you need more
assistance.)
2. Press STAT. Arrow over to CALC. Choose #5 QuadReg.
3. On the home screen: QuadReg L1, L2
4. Press ENTER. You will see the screen at the right showing you
the coefficients and constant of the quadratic equation.
A possible equation is
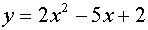 |
|
|


![]()