TI-Nspire - Complex Vector Graph

Complex Vector Graph

The lesson will investigate how to graph complex numbers as vectors on the TI-Nspire.

Get the Screen Ready Because we will be "drawing" on the screen, we need to see the locations of points on the screen. Set up the "dot" grid for this graph. Go to the Graph Screen: , #1 New, #2 AddGraph Temporarily change to "Dot Grid": #2 Hide/Show #3 Show Dot Grid	Put the graph screen into Dot Grid Mode When you move on to a new Graph Screen, the "temporary" dot grid will be gone.
If you want the "Dot Grid" to be permanent for ALL of your graphs, follow the directions at the right, from a Graph Screen, to make a "Settings" change.	To Change ALL graphs to "Dot Grid": From the Graph Screen: #9 Settings Grid DotGrid OK

Move into Vector mode:

#8 Geometry
#1 Points&Lines
#9 Vector

The pencil for drawing will appear.

Graph the complex numbers

3 + 5i

8 + 2i

Place the pencil's dot at the origin.
Lock it in by hitting or .

Drag the pencil's arrow to the desired endpoint. Lock it in place.

Repeat for the second number.

If your pencil "turns off" as you are working with the graph, just repeat the , #8 Geometry, #1 Points&Lines, #9 Vector and you can continue drawing more vectors on the same graph.

Graphically Add:
(3 + 5i) + (8 + 2i)

The sum will be the length, from (0,0), to the vertex of the parallelogram formed by copying the 2 given vector sides.

To copy the sides: Place the pencil dot at the end of one of the 2 vectors and count out the movement pattern from the other vector.

• From the arrow of 3+5i, count 8 to the right and up 2 and stop at that point.
• From the arrow of 8+2i, count 3 to the right and up 5 and stop. You have your parallelogram.

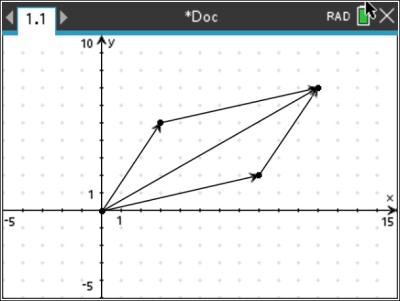
The sum is the complex numbers is 11 + 7i,
(the point at the new vertex of the parallelogram).
The magnitude of this new diagonal vector is
square root of 170.

Table of Contents | MathBits.com | Terms of Use