Table of Contents MathBits.com Terms of Use TI-84+ Web Site
Solving Rational Equations

Rational equations can be solved algebraically by:
      1.  determining the least common denominator (LCD) for the problem,
      2.  multiplying both sides of the equation by the LCD (multiply ALL terms),   
      3.  solving the resulting equation, and
      4.  checking for possible extraneous roots since the derived equation may not be equivalent to the original equation.

While solving algebraically is a skill you need to possess, the calculator can also be used to arrive at a solution. In Algebra 2, however, keep in mind that the calculator is a tool to verify your algebraic solution, and not a replacement for that skill.

A Graphical Solution:
The graphing calculator is a wonderful back-up checking tool to solving rational equations graphically.  This approach is especially helpful in determining extraneous roots.  Consider the examples below.

Example 1:  Solve the following equation algebraically and check graphically.

               rat1

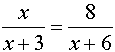
Algebraic Solution:
rat2
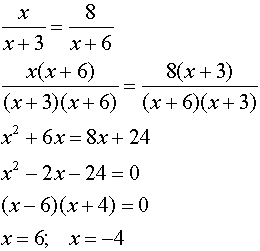
(Yes, you could also use cross multiply to solve this equation.)

Check:
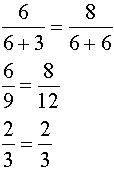rat5		 Check:
rat6

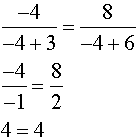Both roots check in this problem.

Notice that the graph shows TWO
intersection points.
Graphical check:
Use template key to enter fractions:
Enter the left side of the equation into f1(x).
Enter the right side of the equation into f2(x).



     Use the INTERSECT option.
, #6 Analyze Graph, #4 Intersection

Checking the two intersection points, gives:
(-4,4) and (6, 2/3)

 

divider
Example 2:  Solve the following equation algebraically and check graphically.

rat9

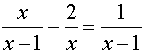
Algebraic Solution:
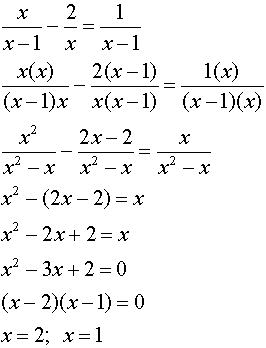rat10
Graphical check:
Use template key to enter fractions:

Enter the left side of the equation into f1(x).
Enter the right side of the equation into f2(x).



   Use the INTERSECT option.
, #6 Analyze Graph, #4 Intersection


A "Zoom In" near x = 1 shows there is not
an intersection point at x = 1.
, #4 Window/Zoom, #3 Zoom In
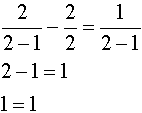Check:
rat11		 Check:
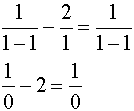
rat12
Division by zero is undefined.  x = 1 is NOT an answer.
x = 1 is an extraneous root.

Hint:  When working with rational equations, it may be difficult to "see" the intersection point if the viewing window is a small representation of the graph. 

You may want to enlarge the viewing window by adjusting the WINDOW settings or by using ZOOM.  You can always quickly return to the standard viewing window by choosing #5 Zoom Standard from Window/Zoom.

Remember:  In this example, you can see that there is only one answer to the equation since there is only one point of intersection. 

Should there be NO points of intersection, the answer will be the empty set.

divider

An "nSolve" Solution:
We have seen, in past topic areas, the use of the calculator's "nSolve" feature to solve equations.
Let's put that feature to work on these rational equations and see what happens.

Before we begin, here are some reminders of where to find stuff when working with nSolve:

Find nSolve in the CATALOG
if you forget where it resides.

Choose tab 1 for an ABC listing.
Arrow down to the word you want.
Typing the first letter will jump down the list.

If you are not familiar with how to type the format for nSolve, the catalog will show you what is needed at the bottom of the screen.
The format shows an optional [Guess].
The guess is not needed.

To get the "such that" vertical bar symbol.

Hitting

gives the Inequality Template:


with the vertical bar in the lower right corner.

When appears,
clicking on the symbol will
give a broad indication of the error.

Alternative Access for nSolve:
Type: the equation = 0

#2 Math Actions,
#1 Solve Numerically

If you are uncertain, choose a wider range.
Hit OK,

 

Example 3:  Solve the following equation using nSolve.

               rat1

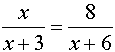
"nSolve" Solution:
1. Start a new Document: Calculator

2. We can activate nSolve() by
, #3 Algebra, #1 Numerical Solve
 or from the Catalog (if you need format info)

3. Enter the equation set = 0:
(subtract the left side from the right side and set = 0)
nSolve (x / (x + 3) - 8 / (x + 6) = 0, x)
(Express the problem in terms of "= 0", and indicate the variable "x" for this problem.)
There is a solution a x = -4.

nSolve (on the non-CAS calculator) finds only ONE solution at a time.

4. How to get the other unique solutions, if they exist:
Another real solution will either be "greater than" or "less than" the first solution found at x = -4.

Let's test and see what happens:
Copy that previous entry again, followed by the "such that" symbol ( | ) and x < -4.
No answer there.
So, let's try x > -4
There is a solution at x = 6.

Now, 6 would be the "next" solution the calculator would encounter as it moves to the right of x = -4. But are there any additional solutions further to the right, beyond x = 6?

The yellow warning triangle is telling us that it is giving a questionable result. In this case, it is not finding a root greater than 6.

We have two solutions: x = -4 and x = 6.

Using nSolve:
  
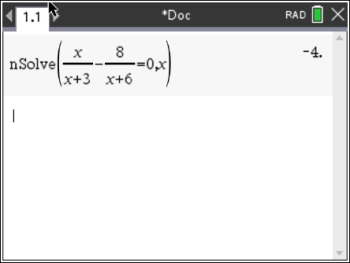
There is a solution at x = -4.
Where are the other solutions, if there are any?

Is there another solution to the left of x = -4? No
nSolve (x / (x + 3) - 8 / (x + 6) = 0, x) | x < -4

Is there another solution to the right of x = -4? Yes
nSolve (x / (x + 3) - 8 / (x + 6) = 0, x) | x > -4
There is a solution at x = 6.

Are there any other solutions beyond x = 6? No
nSolve (x / (x + 3) - 8 / (x + 6) = 0, x) | x > 6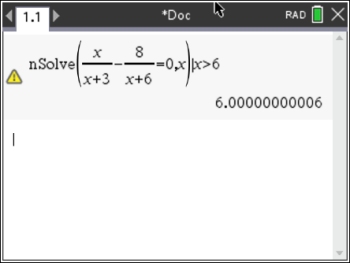

divider
Table of Contents | MathBits.com | Terms of Use